Half Life

Half-life (symbol t1⁄2) is the time required for a quantity to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo, or how long stable atoms survive, radioactive decay. The term is also used more generally to characterize any type of exponential or non-exponential decay. For example, the medical sciences refer to the biological half-life of drugs and other chemicals in the human body. The converse of half-life is doubling time.
The original term, half-life period, dating to Ernest Rutherford's discovery of the principle in 1907, was shortened to half-life in the early 1950s. Rutherford applied the principle of a radioactive element's half-life to studies of age determination of rocks by measuring the decay period of radium to lead-206.
Half-life is constant over the lifetime of an exponentially decaying quantity, and it is a characteristic unit for the exponential decay equation. The accompanying table shows the reduction of a quantity as a function of the number of half-lives elapsed.
Whether or not a given isotope is radioactive is a characteristic of that particular isotope. Some isotopes are stable indefinitely, while others are radioactive and decay through a characteristic form of emission. As time passes, less and less of the radioactive isotope will be present, and the level of radioactivity decreases. An interesting and useful aspect of radioactive decay is half-life, which is the amount of time it takes for one-half of a radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.
Consider the following example. Suppose we have 100.0 g of tritium (a radioactive isotope of hydrogen). It has a half-life of 12.3 y. After 12.3 y, half of the sample will have decayed from hydrogen-3 to helium-3 by emitting a beta particle, so that only 50.0 g of the original tritium remains. After another 12.3 y—making a total of 24.6 y—another half of the remaining tritium will have decayed, leaving 25.0 g of tritium. After another 12.3 y—now a total of 36.9 y—another half of the remaining tritium will have decayed, leaving 12.5 g. This sequence of events is illustrated below”.

Radioactive Decay
During each successive half-life, half of the initial amount will radioactively decay. We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:
where n is the number of half-lives. This expression works even if the number of half-lives is not a whole number.
Example:
The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 44.0 s?
Solution
If we compare the time that has passed to the isotope’s half-life, we note that 44.0 s is exactly 4 half-lives, so using the previous expression, n = 4. Substituting and solving results in the following:
Amount remaining
Less than one-third of a gram of fluorine-20 remains.
Test Yourself
The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 240.0 y?
Answer
0.0375 g
Half-lives of isotopes range from fractions of a microsecond to billions of years. Below table shows it clearly. It is the list of the half-lives of some isotopes.
List of Half-Lives of Various Isotopes
Isotope   Half-Life
3H   12.3 y
14C   5730 y
40K   1.26 × 109 y
51Cr   27.70 d
90Sr   29.1 y
131I   8.04 d
222Rn   3.823 d
235U   7.04 × 108 y
Chemistry Is Everywhere: Radioactive Elements in the Body
You may not think of yourself as radioactive, but you are. A small portion of certain elements in the human body are radioactive and constantly undergo decay. The following table summarizes radioactivity in the normal human body.
Radioactive Isotope
Half-Life (y)   Isotope Mass in the Body (g)   Activity in the Body (decays/s)
40K   1.26 × 109   0.0164   4,340
14C   5,730   1.6 × 10−8   3,080
87Rb   4.9 × 1010   0.19   600
210Pb   22.3   5.4 × 10−10   15
3H   12.3   2 × 10−14   7
238U   4.47 × 109   1 × 10−4   5
228Ra   5.76   4.6 × 10−14   5
226Ra   1,620   3.6 × 10−11   3
The average human body experiences about 8,000 radioactive decays/s.
Most of the radioactivity in the human body comes from potassium-40 and carbon-14. Potassium and carbon are two elements that we absolutely cannot live without, so unless we can remove all the radioactive isotopes of these elements, there is no way to escape at least some radioactivity. There is debate about which radioactive element is more problematic. There is more potassium-40 in the body than carbon-14, and it has a much longer half-life. Potassium-40 also decays with about 10 times more energy than carbon-14, making each decay potentially more problematic. However, carbon is the element that makes up the backbone of most living molecules, making carbon-14 more likely to be present around important molecules, such as proteins and DNA molecules. Most experts agree that while it is foolhardy to expect absolutely no exposure to radioactivity, we can and should minimize exposure to excess radioactivity.
Half-Life Calculations:
Information on the half-life of an isotope can be used to calculate how much radioactivity of that isotope will be present after a certain period of time. There is a formula that allows calculation at any time after the initial count, but we are just going to look at loss of activity after different half-lives. The isotope I-125 is used in certain laboratory procedures and has a half-life of 59.4 days. If the initial activity of a sample of I-125 is 32,000 cpm, how much activity will be present in 178.2 days? We begin by determining how many half-lives are represented by 178.2 days:
frac{178.2 text{days}}{59.4 text{days}/ text{half-life}} = 3 text{half-lives}
Then we simply count activity:
text{initial activity} (t_0) &= 32,000 text{cpm} \text{after one half-life} &= 16,000 text{cpm} \text{after two half-lives} &= 8,000 text{cpm} \text{after three half-lives} &= 4,000 text{cpm}
Be sure to keep in mind that the initial count is at time zero (t_0) and we subtract from that count at the first half-life. The second half-life has an activity of half the previous count (not the initial count).
For the more mathematically inclined, the following formula can be used to calculate the amount of radioactivity remaining after a given time:
N_t = N_0 times (0.5)^{text{number of half-lives}}
where N_t = text{activity at time} t
N_0 = text{initial activity at time} = 0
If we have an initial activity of 42,000 cpm, what will the activity be after four half-lives?
N_t &=N_0(0.5)^4 \&=(42,000)(0.5)(0.5)(0.5)(0.5) \&=2625 text{cpm}
Half-lives of different elements vary considerably, as shown in Table below:
Isotope Half-Lives
Isotope   Decay Mode   Half-Life
Cobalt-60   beta   5.3 years
Neptunium-237   alpha   2.1 million years
Polonium-214   alpha   0.00016 seconds
Radium-224   alpha   3.7 days
Tritium (H-3)   beta   12 years
We have talked about the activity and decay of individual isotopes. In the real world, there is a decay chain that takes place until a stable end-product is produced. For U-238, the chain is a long one, with a mix of isotopes having very different half-lives. The end of the chain resides in lead, a stable element that does not decay further.
Decay chain of Uranium-238.
The half-life of a diminishing substance is the time it takes for the amount of substance present to go halfway from some initial value to zero. It is thus an indication of how fast the diminishment process proceeds or of the rate or rapidity of that process. The faster the process, the shorter the substance’s half-life is.

The rates of some biological processes, such as the elimination of drugs from the body, can be characterized by their half-lives, because it takes the same amount of time for half of the drug to disappear no matter how much there was to begin with. Processes of this kind are called first-order processes. On the other hand, the speeds of many chemical reactions depend on the amounts of the various substances that are present, so their rates cannot be expressed in terms of half-lives; more complicated mathematical descriptions are necessary.

Half-lives are most often heard of in connection with radioactive decay. In this process, the number of atoms of a radioisotope (a radioactive isotope) is constantly diminishing because the atoms are transforming themselves into other kinds of atoms. (In this sense, the word “decay” does not mean to rot; it means to diminish in amount.) If a particular radio-isotope has a half-life of one hour, for example, then at 3 PM there will be only half as many of the original species of radioisotope atoms remaining as there were at 2 PM; at 4 PM, there will be only half as many as there were at 3 PM, and so on. The amount of the radioactive material thus gets smaller and smaller, but it never disappears entirely. This is an example of what is known as exponential decay.

The half-life of a radioisotope is a characteristic of its nuclear instability, and it cannot be changed by ordinary chemical or physical means. Known radioisotopes have half-lives that range from tiny fractions of a second to quadrillions of years. Waste from the reprocessing of nuclear reactor fuel contains radioisotopes of many different half-lives, and can still be at a dangerously high level after hundreds of years.

The mathematical equation which describes how the number of atoms, and hence the amount of radioactivity, in a sample of a pure radioisotope decreases as time goes by, is called the radioactive decay law. It can be expressed in several forms, but the simplest is this: log P = 2 - 0.301 t/t12. In this equation, P is the percentage of the original atoms that still remain after a period of time t, and t12 is the half-life of the radioisotope, expressed in the same units as t. In other words: To get the logarithm of the percentage remaining, divide t by the half-life, multiply the result by 0.301, and subtract that result from 2.
Half-life
As defined by geophysicists, the half-life (or half-value period) of a substance is the time required for one-half of the atoms in any size sample to radioactively decay.

Radioactive elements have different isotopes that decay at different rates. As a result, half-life varies with regard to the particular isotope under consideration. Some isotopes have very short half-lives, for example oxygen-14 has a half-life of only 71 seconds, some are even shorter—with values measured in millionths of a second not being uncommon. Other elements' isotopes can have a much longer half-life, thallium-232 has a half-life of 1.4 × 10 10 years and carbon-14 has a half-life of 5,730 years. This latter figure is used as the basis of radiocarbon dating.

While living, an organism takes in an amount of carbon-14 at a relatively constant rate. Once the organism dies no more carbon-14 is taken in and the amount of carbon-14 present overall starts to decrease, decreasing by half every 5,730 years. By measuring the ratio of carbon-12 to carbon-14 an estimate of the date when carbon-14 stopped being assimilated can be calculated. This figure can also be obtained by comparing the levels of radioactivity of the test material to that of a piece of identical material that is fresh. Other radioactive elements can be used to date older, inorganic materials (e.g., rocks).

Strontium-90 has a half-life of 29 years. If starting with a 2.2 lb (1 kg) mass of strontium-90, then after 29 years there will only be 1.11 lb (0.5 kg) of strontium-90 remaining. After a further 29 years there will only be 0.55 lb (0.25 kg). Strontium-90 decays to give yttrium-90 and one free electron. Half-life is independent of the mass of material present.

The half-life (t1/2) of a material can be calculated by dividing 0.693 by the decay constant (which is different for different radionucleotides). The decay constant can be calculated by dividing the number of observed disintegrations per unit time by the number of radioactive nuclei in the sample. The decay constant is usually given the symbol k or λ.

The half-life of a material is a measure of how reactive it is either in terms of radioactive decay or in participation in specific reaction
Half-life
The half-life of a process is an indication of how fast that process proceeds—a measure of the rate or rapidity of the process. Specifically, the half-life is the length of time that it takes for a substance involved in that process to diminish to one-half of its initial amount. The faster the process, the less time it will take to use up one-half of the substance, so the shorter the half-life will be.

Half-lives are most often heard of in connection with radioactive decay—a first-order process in which the number of atoms of a radioisotope (a radioactive isotope ) is constantly diminishing because the atoms are transforming themselves into other kinds of atoms. (In this sense, the word "decay" does not mean to rot; it means to diminish in amount.) If a particular radioisotope has a half-life of one hour, for example, then at 3 p.m. there will be only half as many of the original species of radioisotope atoms remaining as there were at 2 p.m.; at 4 p.m., there will be only half as many as there were at 3 p.m., and so on. The amount of the radioactive material thus gets smaller and smaller, but it never disappears entirely. This is an example of what is known as exponential decay.

Half-life
A term primarily used to describe the physical half-life, how radioactive decay processes cause unstable atoms to be transformed into another element, but can also refer to the biological half-life of substances that are not radioactive.

Specifically, the physical half-life is the time required for half of a given initial quantity to disappear (or be converted into something else). This description is useful because radioactive decay proceeds in such a way that a fixed percentage of the atoms present are transmuted during a given period of time (a second, a minute, a day, a year). This means that many atoms are removed from the population when the total number present is high, but the number removed per unit of time decreases quickly as the total number falls.

For all practical purposes, the number of radioactive atoms in a population never reaches zero because decay affects only a fraction of the number present. Some infinitesimal number will still be present even after an infinite number of half-lives because with each time period half of what was present before decays and is lost from the sample. Therefore, determining the point at which half of the original number disappears (the half-life) is usually the most accurate way of describing this process
Half-life is a measurement of the time it takes for one-half of a radioactive substance to decay (in this sense, decay does not mean to rot, but to diminish in quantity).

The atoms of radioactive substances, such as uranium and radium, spontaneously break down over time, transforming themselves into atoms of another element. In the process, they give off radiation, or energy emitted in the form of waves. An important feature of the radioactive decay process is that each substance decays at its own rate. The half-life of a particular substance, therefore, is constant and is not affected by any physical conditions (temperature, pressure, etc.) that occur around it.

Because of this stable process, scientists are able to estimate when a particular substance was formed by measuring the amount of original and transformed atoms in that substance. For example, the amount of carbon in a fossil sample can be measured to determine the age of that fossil. It is known that the radioactive substance carbon-14 has a half-life of 5,570 years. The half-lives of other radioactive substances can range from tiny fractions of a second to quadrillions of year

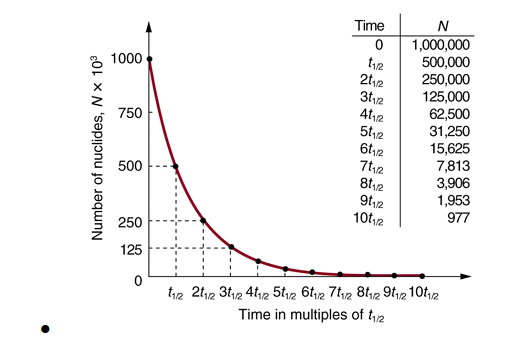
a radioactive decay graph of number of nuclides in thousands versus time in multiples of half-life. The number of radioactive nuclei decreases exponentially and finally approaches zero after about ten half-lives. Radioactive decay reduces the number of radioactive nuclei over time. In one half-life t1/2, the number decreases to half of its original value. Half of what remains decay in the next half-life, and half of those in the next, and so on. This is an exponential decay, as seen in the graph of the number of nuclei present as a function of time.